Conjunto Z
Multiplicación y División en Z

La regla que se utiliza es la misma para multiplicar que para dividir.¿ CÓMO SE HACE?. Multiplico números y luego multiplico los signos de acuerdo a la siguiente tabla:
+ · + = + - · - = +
+ · - = - - · + = -
Ej: 5 · 10 = 50
12 · -4 = -48
-7 . 2 = -14
Siempre se deben multiplicar o dividir los números y luego aplicar las reglas de signos para dichas operaciones.
Estructura de los números enteros:
Los enteros con la adición y la multiplicación forman una estructura algebraica llamada anillo. Pueden ser considerados una extensión de los números naturales y un subconjunto de los números racionales (fracciones). Los números enteros son subconjunto de los números racionales o fracciones, puesto que cada número entero puede ser considerado como una fracción cuyo denominador es el número uno.
Los números enteros pueden ser sumados y/o restados, multiplicados y comparados. Si la división es exacta, también pueden dividirse dentro del mismo conjunto de los enteros. La razón principal para introducir los números negativos sobre los números naturales es la posibilidad de resolver ecuaciones del tipo:
a + x = b
para la incógnita x.
Matemáticamente, el conjunto de los números enteros con las operaciones de suma y multiplicación, constituye un anillo conmutativo y unitario. Por otro lado, , donde es el orden usual sobre , es un conjunto completamente ordenado sin cota superior o inferior: los enteros no tienen principio ni fin. El conjunto de los números enteros se representa mediante (el origen del uso de Z es el alemán Zahlen 'números').
Construcción formal de los enteros a partir de los naturales:
Un número entero negativo puede ser definido mediante la diferencia de dos números naturales. Por ejemplo − 3 = 5 − 8, de donde puede asociarse el número − 3 con el par ordenado (5,8) de números naturales. Sin embargo, debido a que (4,7) y una infinidad más de pares ordenados dan como resultado − 3 al restar sus componentes, no puede decirse simplemente que − 3 = (5,8). Lo que puede hacerse, es incluir todos los pares ordenados de números naturales, que dan como resultado − 3 al restar sus componentes, dentro de un solo conjunto, o, más exactamente, dentro de una clase de equivalencia.
La representación de los números enteros es :
Z = {... -2,-1,0,+1,+2,... }
Dentro de los números enteros (están completos ) o sea no son decimales como 2,5 ; 1,5 ; 3,5 ; etc. sino que son : 0,1,2,3,4,5,6,7,+1,+2,+3,+4,+5,+6,+7, positivos ( teniendo el signo o no ) .También dentro de ellos están los negativos como se puede apreciar en la notación simbólica.
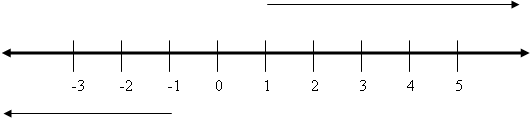
-1,-2,-3,-4,-5,-6,-7,-8,....
Decíamos que es el cociente de una división exacta porque al dividir 20/5 obtenemos como resultado 4 que no es más que el cociente que pertenece a los números enteros y también naturales . La diferencia entre ENTEROS (Z) y NATURALES (N) es que los enteros contienen números negativos y los naturales no contienen números negativos. Otra diferencia es que los enteros llevan visible el signo positivo (+) , mientras que los naturales lo llevan invisible, es decir , SOBREENTENDIDO. Naturales: 0,1,2,3,4,5,6,7,...
Enteros: 0,+1,+2,+3,+4,+5,+6,+7,... ; el cero como dije en otra ocasión no posee signo ni positivo ni negativo es neutro.
Los números enteros positivos se hallan a la derecha del cero en la recta numérica.
Los números enteros negativos se hallan a la izquierda del cero en la recta numérica.
-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7

Operaciones en Z (con enteros positivos y negativos)
Para poder realizar las operaciones en el conjunto de los números enteros (Z) debes memorizar las siguientes reglas (son fáciles; sólo requieren de práctica).
Suma en Z (Conjunto de Números Enteros positivos y negativos):
Existen únicamente dos casos: números de igual signo y números con signo distinto. Las reglas a memorizar son las siguientes:
a) Números de igual signo: Cuando dos números tiene igual signo se debe sumar y conservar el signo.
Ej :-3 + -8 = - 11 ( sumo y conservo el signo)
12 + 25 = 37 ( sumo y conservo el signo)

No hay comentarios:
Publicar un comentario